麦卡托投影法

数学计算

  地图上纵向方位（图中的横轴）和纬度（图中的纵轴）的关系。

下列公式定义在使用麦卡托投影的地图中，从纬线φ和经线λ（其中λ0是地图的中央经线）如何推导为坐标系中的点坐标x和y。

这是古德曼函数的逆推导：

这是古德曼函数：

比例尺与纬度φ的正割成比例，越趋向极地（φ = ±90°）面积变形越大。此外，由公式可知，极点处的y值为正负无穷大。

公式推导

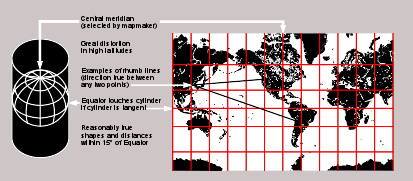
麦卡托投影是一种等角投影。

假设地球为正球形。（实际上并非为正球形，而是有扁率的，但制作小比例尺地图时误差可忽略不计。若需更精确，可插入等角纬线。）我们需要将经纬度坐标（λ, φ）转换为笛卡尔坐标(x, y)，求以赤道为基准的切柱面投影（即x = λ），并保持形状不变，故：

从 x = λ 可知

给出

因此，y是φ的唯一函数，且可得到 y ′ = sec ⁡ ⁡ --> φ φ --> {\displaystyle y"=\sec \varphi } ，由积分表

在地图中φ = 0得到y = 0，所以取C = 0.

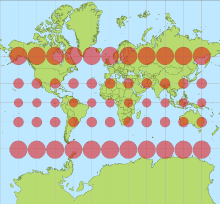
  以麦卡托投影法绘制的地图。

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。