收敛洛朗系列

复系数洛朗级数是复分析中的一个重要工具，尤其在研究函数奇点附近的行为时。

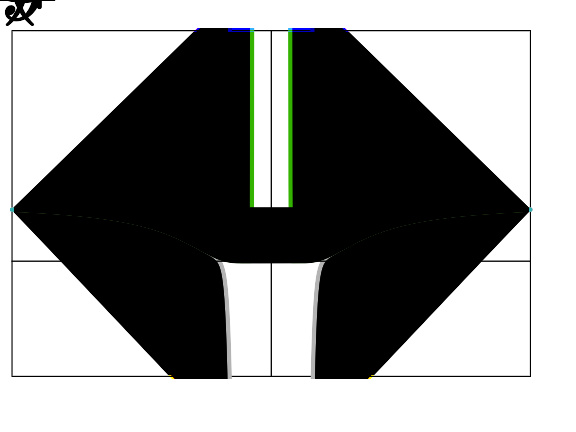
e和洛朗近似：见文中解释。随着洛朗级数负次数的增长，图像接近正确的函数。

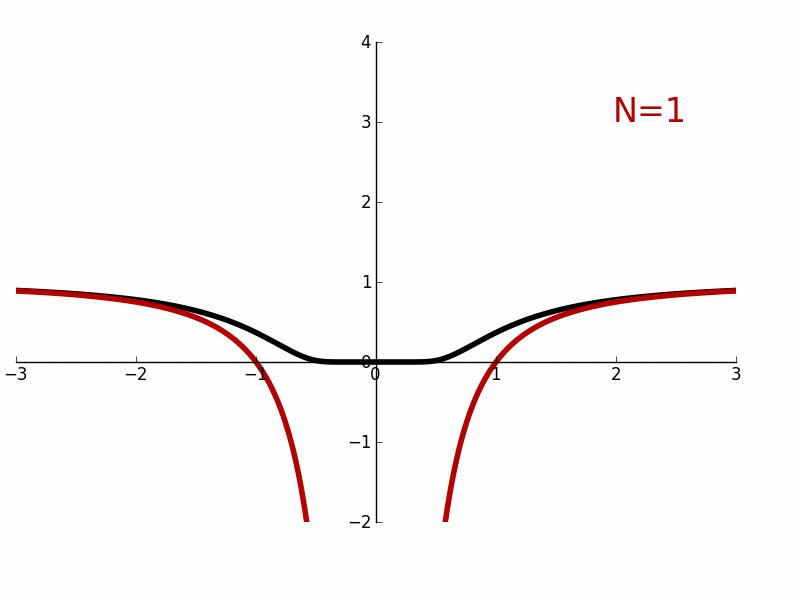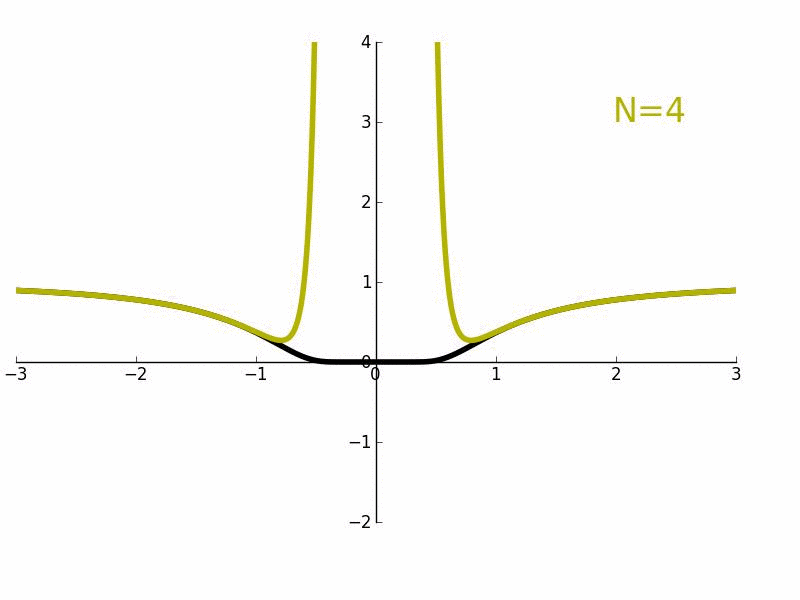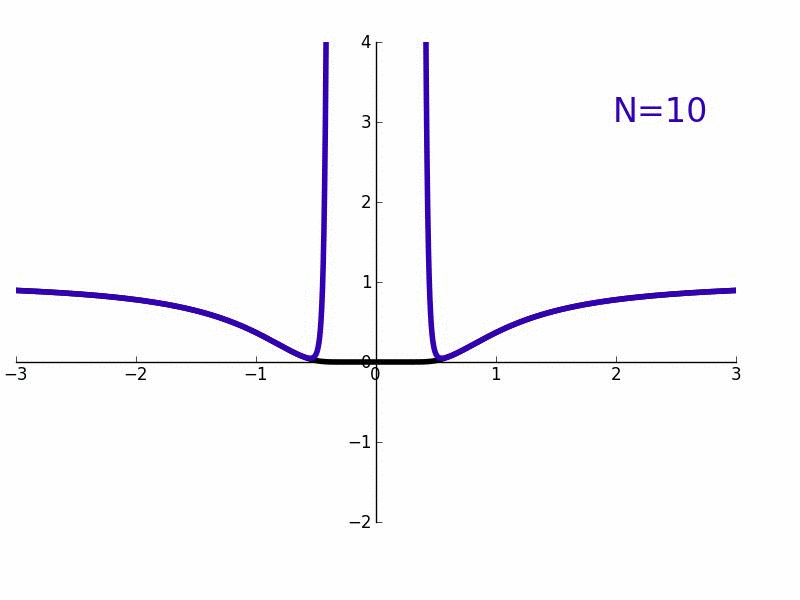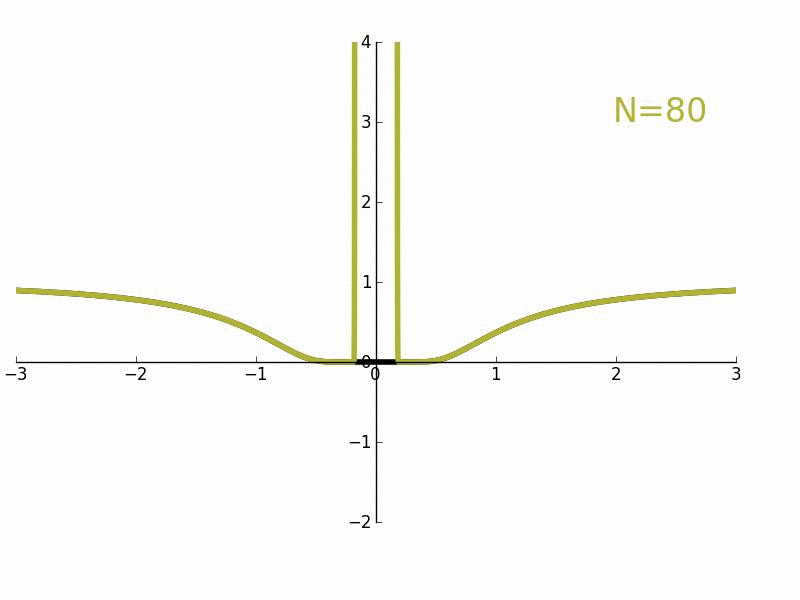
e和洛朗近似的负次数的增长。奇点零的邻域不能被近似。

考虑例如函数f(x)=e− − -->1/x2{\displaystyle f(x)=e^{-1/x^{2}}}，它的f(0)=0{\displaystyle f(0)=0} 。作为实变函数，它是处处无穷可微的；但作为一个复变函数，在x = 0处不可微。用−1/x替换指数函数的幂级数展开式中的x，我们得到其洛朗级数，对于除了奇点X = 0以外的所有复数，它都收敛并等于ƒ(x)。旁边的图显示了e（黑色）和它的洛朗近似

对于N = 1, 2, 3, 4, 5, 6, 7到50。当N → ∞，近似对除了奇点x = 0处的所有复数x都很精确。

更一般地，洛朗级数可以用来表达定义在圆环上的全纯函数，就像幂级数被用于表达一个圆盘上定义全纯函数一样。

参看

Z转换

傅立叶级数

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。