伽罗瓦，高斯，阿贝尔三个人相比 谁的数学天赋更高

　　历史上有非常多的杰出数学家，若论成就，很多榜单都把高斯排在第一。而实际上数学是一门非常吃天赋的科学，有些人年纪轻轻就已经完成了很多人一生都达不到的学术成就。所以说如若我们抛开成就不谈，都有哪些数学天赋极高的天才呢?我们一起来看看。

　　伽罗瓦

　　埃瓦里斯特·伽罗瓦，1811年10月25日生，法国数学家。伽罗瓦16岁才开始系统学习数学，18岁就创立了群论。这是当代代数与数论的基本支柱之一。它直接推论的结果十分丰富：他系统化地阐释了为何五次以上之方程式没有公式解，而四次以下有公式解。然后他漂亮地证明高斯的论断：若用尺规作图能作出正 p 边形，p 为质数的充要条件为 。(所以正十七边形可做图)。另外 他解决了古代三大作图问题中的两个：“不能任意三等分角”，“倍立方不可能”。

　　而令人惋惜的是，他在世时在数学上研究成果的重要意义没被人们所认识，曾呈送科学院3篇学术论文，均被退回或遗失。后转向政治，支持共和党，曾两次被捕。21岁时死于一次决斗。所以以上的成就不过是短短五六年里面取得的。伽罗瓦天赋之高，深不可测，古今难寻。

　　高斯

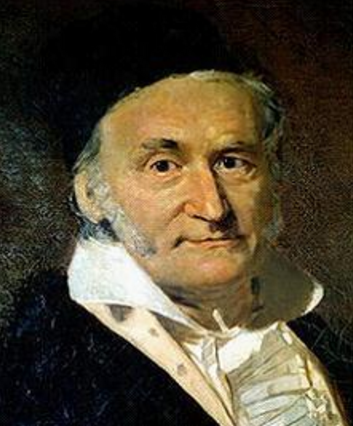
　　高斯19岁就发现了正十七边形的尺规作图法， 解决了自欧几里德以来悬而未决的一个难题。同年，发表并证明了二次互反律。这是他的得意杰作，一生曾用八种方法证明，称之为"黄金律" 。高斯在29岁就得到非欧几何的原理。他还深入研究复变函数，建立了一些基本概念发现了著名的柯西积分定理。当然他还有很多卓绝的成就，不过只看天赋的话，他也是最顶尖的一批数学家了。

　　阿贝尔

　　尼尔斯·亨利克·阿贝尔(1802年8月5日-1829年4月6日)，挪威数学家，在很多数学领域做出了开创性的工作。他最著名的一个结果是首次完整给出了高于四次的一般代数方程没有一般形式的代数解的证明。这个问题是他那时最著名的未解决问题之一，悬疑达250多年。他也是椭圆函数领域的开拓者，阿贝尔函数的发现者。尽管阿贝尔成就极高，却在生前没有得到认可，他的生活非常贫困，死时只有27岁。