拉普拉斯-龙格-楞次矢量

概论

在一个物理系统里，在任意保守的有心力的作用下（参阅保守力），一个粒子的运动，都会拥有至少四个运动常数；能量与角动量L{\displaystyle \mathbf {L} }的三个分量皆为运动常数。粒子的轨道被限制于一个平面。粒子的动量p{\displaystyle \mathbf {p} }和从力中心点的位置到粒子位置的位移r{\displaystyle \mathbf {r} }（参阅图1）。粒子的运动平面垂直于角动量L{\displaystyle \mathbf {L} }。用方程表示，

LRL矢量A{\displaystyle \mathbf {A} }，也肯定地包含于粒子的运动平面。可是，只有当有心力遵守平方反比定律时，A{\displaystyle \mathbf {A} }才是常数矢量。对于别种有心力，A{\displaystyle \mathbf {A} }不是常数矢量，其大小与方向都会改变。假若有心力近似地遵守平方反比定律，则A{\displaystyle \mathbf {A} }的大小近似常数，而方向会缓慢地转动。对于所有的有心力，可以定义一个广义LRL矢量，但是，这广义矢量通常并没有解析解，假若有，也会是一个非常复杂的函数。

历史

在重要的开普勒问题中，LRL矢量A{\displaystyle \mathbf {A} }是一个运动常数，时常用来描述天文轨道，例如行星的运动。然而，物理学家对它并不熟悉，这很可能是因为与动量与角动量相比，它比较难以被直觉地理解内涵的物理。因此，在过去三个世纪里，它曾被重复地发现过许多次。1710年，在一个不著名的意大利学刊里，雅各布·赫尔曼最先发表了关于LRL矢量的论文。在推导一个轨道方程的过程中，他计算出LRL矢量的大小， A{\displaystyle A}是保守的；并且推导出此案例与椭圆轨道离心率的关系。稍后，赫尔曼把这结果告诉约翰·伯努利，他的恩师。伯努利又更进一步地推导出LRL矢量的方向。这样，LRL矢量得到了它的现代形式。所以，不容质疑地，LRL矢量是赫尔曼和伯努利共同发现的。

在那个世纪末尾，皮埃尔-西蒙·拉普拉斯又重新地发现了LRL矢量的保守性；稍微不同地，他的导引使用的是分析方法，而不是几何方法。十九世纪中叶，威廉·哈密顿推导出全等的离心率矢量。他用离心率矢量来证明，在平方反比有心力作用下，速端曲线显示出，粒子动量矢量的头部呈圆形移动 （参阅图3）。二十世纪初，约西亚·吉布斯，应用矢量分析，推导出同样的矢量。后来，卡尔·龙格将吉布斯的导引，纳入自己所写的一本广受欢迎的，关于矢量的，德文教科书内，成为其中的一个例题。1924年，威尔汉·楞次发表了一篇关于氢原子的旧量子论的论文。在这篇论文中，他引用龙格所写的教科书的例题为参考。1926年，沃尔夫冈·泡利用LRL矢量与矩阵力学，而不是薛定谔方程，来推导氢原子的光谱。这杰作说服了大多数物理学家，使他们觉得量子力学理论是正确的。

数学定义

图1:在平方反比有心力的作用下，一个移动中的粒子，在椭圆轨道的四点（标记为1, 2, 3,与4）的LRL矢量A{\displaystyle \mathbf {A} }（红色表示）。力中心点表示为一个小黑点；从这黑点，位置矢量r{\displaystyle \mathbf {r} }（黑色表示）以径向方向指出。角动量L{\displaystyle \mathbf {L} }垂直于轨道的平面。共面的矢量p× × -->L{\displaystyle \mathbf {p} \times \mathbf {L} }与mkr^ ^ -->{\displaystyle mk{\hat {\mathbf {r} }}}分别用蓝色与绿色表示。LRL矢量A{\displaystyle \mathbf {A} }是一个运动常数矢量

平方反比有心力F(r){\displaystyle \mathbf {F} (r)}可以表达为

其中，k{\displaystyle k}是比例常数，r^ ^ -->=rr{\displaystyle \mathbf {\hat {r}} ={\frac {\mathbf {r} }{r}}}是单位矢量，r{\displaystyle \mathbf {r} }是粒子的位置矢量，r{\displaystyle r}是r{\displaystyle \mathbf {r} }的大小。

感受到此力的作用，一个粒子的轨道运动，其LRL矢量的数学定义方程为

其中，m{\displaystyle m}是粒子的质量，p{\displaystyle \mathbf {p} }是动量，L=r× × -->p{\displaystyle \mathbf {L} =\mathbf {r} \times \mathbf {p} }是角动量。

由于平方反比有心力为保守力，能量E=p22m− − -->kr{\displaystyle E={\frac {p^{2}}{2m}}-{\frac {k}{r}}}是运动常数：

再者，角动量L{\displaystyle \mathbf {L} }也是保守的，可以决定粒子移动平面的取向。因为p× × -->L{\displaystyle \mathbf {p} \times \mathbf {L} }与r{\displaystyle \mathbf {r} }都垂直于L{\displaystyle \mathbf {L} }，所以，LRL矢量A{\displaystyle \mathbf {A} }垂直于角动量；A{\displaystyle \mathbf {A} }包含于轨道的平面。

这个单独粒子的LRL矢量定义，也可以延伸至像开普勒问题一类的二体问题，只需要设定质量m{\displaystyle m}为二个物体的约化质量，设定位置矢量r{\displaystyle \mathbf {r} }为二个物体之间的相对位置矢量。

同样的运动常数可以有很多种不同的表述．最常见的一种牵涉到离心率矢量。定义离心率矢量e{\displaystyle \mathbf {e} }为LRL矢量与mk{\displaystyle mk}的除商：

开普勒轨道导引

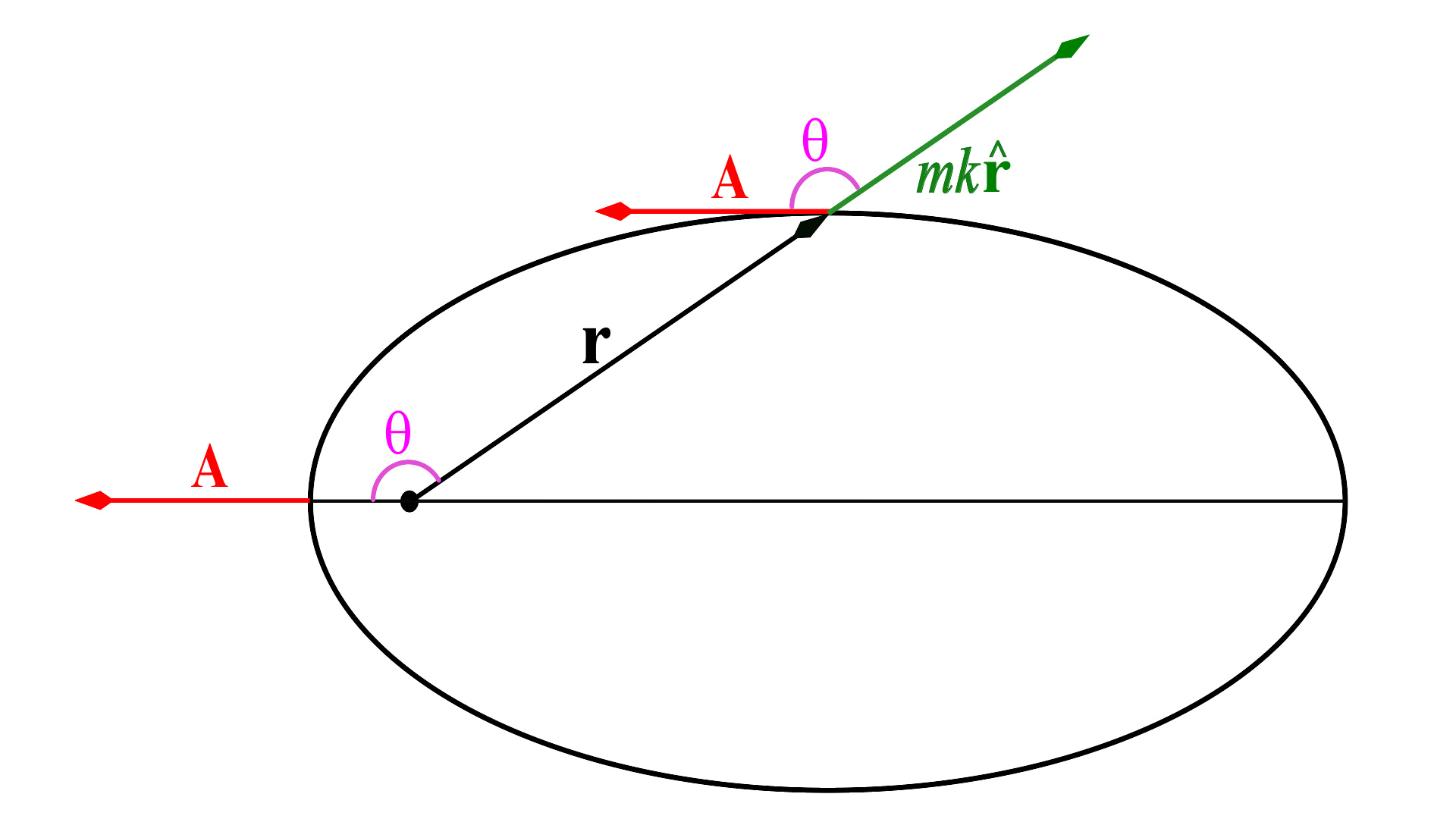
图2：这是图1的简化版，角θ θ -->{\displaystyle \theta }定义为A{\displaystyle \mathbf {A} }与r{\displaystyle \mathbf {r} }之间的夹角。

开普勒问题的运动轨道，其形状与取向，可以用LRL矢量决定。A{\displaystyle \mathbf {A} }与r{\displaystyle \mathbf {r} }的内积为

其中，θ θ -->{\displaystyle \theta }为A{\displaystyle \mathbf {A} }与r{\displaystyle \mathbf {r} }之间的夹角。

置换其三重积，

所以，

编排成圆锥曲线的方程形式：

离心率e{\displaystyle e}为

开普勒轨道与能量的关系可以由LRL矢量推导出。A{\displaystyle \mathbf {A} }与自己的内积为

所以，

稍微编排，离心率的平方e2{\displaystyle e^{2}}是能量E{\displaystyle E}的函数：

假若能量E{\displaystyle E}是负值的（束缚轨道），则离心率小于1，这轨道是椭圆形轨道。相反地，假若能量是正值的（非束缚轨道，又称为散射轨道）则离心率大于1，这轨道是双曲线轨道。最后，假若能量等于零，则离心率等于1，这轨道是抛物线轨道。对于所有状况，LRL矢量与圆锥曲线的对称轴平行，而且从力中心点指向近拱点。

圆形的速端曲线

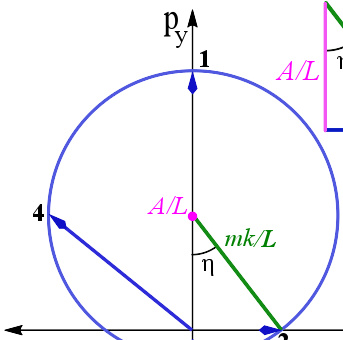
图3 :在平方反比有心力作用下，随着粒子的轨道运动，使用速端曲线图，固定动量矢量p{\displaystyle \mathbf {p} } (蓝色表示)的尾部于原点，则其头部呈圆形移动。四个标记的点对应于图1的四点。圆形的中心是在py-轴，py-坐标为A/L{\displaystyle A/L}（以品红色表示），半径是mk/L{\displaystyle mk/L}（以绿色表示）。

假设一个粒子在做轨道运动。其速度矢量的物理行为可以用速端曲线显示出来，而动量是速度乘以质量。所以，速端曲线也可以显示出动量的物理行为。在平方反比有心力作用下，速端曲线（图3）显示出，粒子的动量矢量的头部呈圆形移动；这事实可以用LRL矢量A{\displaystyle \mathbf {A} }与角动量L{\displaystyle \mathbf {L} }的保守性来证明。计算L{\displaystyle \mathbf {L} }与A{\displaystyle \mathbf {A} }的叉积：

设定xyz参考系的圆点在力中心点，L{\displaystyle \mathbf {L} }与z-轴同方向，x-轴与半长轴同轴。则

换句话说，动量p{\displaystyle \mathbf {p} }的头部被限制于一个圆圈；圆圈的半径为mk/L{\displaystyle mk/L}，圆心为(0, A/L){\displaystyle (0,\ A/L)}。如图3所示，圆形的动量速端曲线毫无疑问地显示出开普勒问题的对称性。

夹角η η -->{\displaystyle \eta }的一边是点2与圆心的连线，另一边是负py-轴。很显然地，离心率等于cos⁡ ⁡ -->η η -->{\displaystyle \cos \eta }。为了简化运算，在这里提出一个很有用的变量p0=2m|E|{\displaystyle p_{0}={\sqrt {2m\left|E\right|}}}。

运动常数与超级可积分性

在开普勒问题里，两个矢量A{\displaystyle \mathbf {A} }，L{\displaystyle \mathbf {L} }与一个标量E{\displaystyle E}加起来一共有七个常数标量。它们之间的相关性表达于A⋅ ⋅ -->L=0{\displaystyle \mathbf {A} \cdot \mathbf {L} =0}与A2=m2k2+2mEL2{\displaystyle A^{2}=m^{2}k^{2}+2mEL^{2}}这两个公式。因为A{\displaystyle \mathbf {A} }的大小可以由角动量L{\displaystyle \mathbf {L} }与能量E{\displaystyle E}计算出来。再者，A{\displaystyle \mathbf {A} }必须垂直于L{\displaystyle \mathbf {L} }。所以，A{\displaystyle \mathbf {A} }只能贡献1个运动常数。

由于有上述两个关系公式，这物理系统一共有五个独立的运动常数。这结果与设定粒子轨道所需的六个初始条件（粒子的初始位置矢量与初始速度矢量，每一个矢量有三个分量）相符合，原因是运动常数不涉及初始时间（视六个初始条件函数的参数为自变量初始时间。用其中的一个初始条件函数除去这自变量；将此初始条件函数当作一个自变量，则剰余五个初始条件函数，函数的参数为新自变量）。

因为运动方程是二阶微分方程，一个拥有d{\displaystyle d} 自由度的物理系统，需要2d{\displaystyle 2d}个初始条件来设定解答。由于运动常数不涉及初始时间，这物理系统最多只能拥有2d− − -->1{\displaystyle 2d-1}个运动常数。一个拥有超过d{\displaystyle d}个运动常数的物理系统称为超级可积分系统；而一个拥有2d− − -->1{\displaystyle 2d-1}个运动常数的物理系统称为最大超级可积分系统。哈密顿-亚可比方程的解答，采用任意一种坐标系统，最多只能求得d{\displaystyle d}个运动常数。

开普勒问题拥有三个自由度（d=3{\displaystyle d=3}）与五个运动常数；开普勒问题的系统是最大超级可积分系统；采用球坐标或抛物线坐标，哈密顿－亚可比方程都是可积分的；这论据，稍后会有详细的解释。最大超级可积分系统可以用对易关系来量子化，这论据，稍后也会又更明了的说明。

在摄动势下的系统演化

图5：椭圆轨道的慢进动，离心率e=0.667{\displaystyle e=0.667}。假若，引性的有心力与平方反比定律稍微有点不同，类似的进动就会发生。

只有在一个标准的平方反比有心力下，粒子的LRL矢量A{\displaystyle \mathbf {A} }是保守的。对于大多数的实际问题，例如行星运动，作用力并不会完全地遵守平方反比定律，而可能会含有别种摄动的有心力；称其负值不定积分为摄动势，标记为h(r){\displaystyle h(r)}。在这种状况下，LRL矢量会缓慢地转动于轨道平面，相应于轨道的慢进动。假若摄动势h(r){\displaystyle h(r)}为一个保守的连心势，也就是说，总能量E{\displaystyle E}与角动量L{\displaystyle \mathbf {L} }都是保守的，则粒子的运动仍旧包含于一个垂直于L{\displaystyle \mathbf {L} }的平面，大小A{\displaystyle A}仍旧是保守的。摄动势h(r){\displaystyle h(r)}可以是任何形式的函数。但是，摄动值应该显著地弱于主连心势。一个典形的摄动势可以表示为

其中，h{\displaystyle h}是摄动势强度，整数n≤ ≤ -->2{\displaystyle n\leq 2}。

用正则摄动理论与作用量-角度坐标，可以直接地推导出LRL矢量的转动率是

其中，T{\displaystyle T}是轨道周期，恒等式Ldt=mr2dθ θ -->{\displaystyle Ldt=mr^{2}\mathrm {d} \theta }转变时间积分为角积分（如图5）。角括号表达式⟨ ⟨ -->h(r)⟩ ⟩ -->{\displaystyle \langle h(r)\rangle }是周期平均摄动势；也就是说，物体绕轨道一个公转的平均摄动势。取平均值可以减少转动率的变动。

这方法曾经被用来证实爱因斯坦的广义相对论。广义相对论在常见的牛顿万有引力项目外，又添加了一项小的反立方摄动。

将此函数代入积分。再代入r{\displaystyle r}与θ θ -->{\displaystyle \theta }的关系公式

就可以计算出这非牛顿摄动所产生的近拱点进动率:

计算出的答案准确地符合实验观测到的水星进动数据和双重脉冲星数据。这与实验数据一致的结果被认为是广义相对论的强证。

泊松括号

角动量L{\displaystyle \mathbf {L} }的三个分量Li{\displaystyle L_{i}}的泊松括号是

其中，指标i, j=1, 2, 3{\displaystyle i,\ j=1,\ 2,\ 3}代表直角坐标系的三个坐标(x, y, z){\displaystyle (x,\ y,\ z)}，ϵ ϵ -->ijs{\displaystyle \epsilon _{ijs列维-奇维塔符号塔符号；在这里，为了避免与力强度的标记k{\displaystyle k}发生混淆，采用s{\displaystyle s}为连加运算的指标。

定义一个与LRL矢量成比例的矢量D{\displaystyle \mathbf {D} }为

矢量D{\displaystyle \mathbf {D} }与角动量L{\displaystyle \mathbf {L} }的单位相同。D{\displaystyle \mathbf {D} }与L{\displaystyle \mathbf {L} }的泊松括号为

矢量D{\displaystyle \mathbf {D} }与自己的泊松括号跟总能量E{\displaystyle E}的正负号有关；也就是说，跟是否总能量E{\displaystyle E}是正值（在平方反比有心力作用下，产生开放的双曲线轨道），或负值（在平方反比有心力作用下，产生闭合地椭圆轨道）有关。假若总能量E{\displaystyle E}是正值，泊松括号是

反之，假若总能量E{\displaystyle E}是负值，泊松括号是

由于以下这三个泊松括号方程，

如果总能量E{\displaystyle E}是负值，则可确定开普勒问题的对称群是四维的旋转群SO(4)。

假若总能量E{\displaystyle E}是负值，卡西米尔不变量C1, C2{\displaystyle C_{1},\ C_{2}}定义为

而且，卡西米尔不变量与D{\displaystyle \mathbf {D} }的每一个分量的泊松括号皆为零：

还有，卡西米尔不变量与L{\displaystyle \mathbf {L} }的每一个分量的泊松括号皆为零：

既然两个矢量D{\displaystyle \mathbf {D} }与L{\displaystyle \mathbf {L} }永远是互相垂直的，C2{\displaystyle C_{2}}明显地是零。可是，另外一个不变量C1{\displaystyle C_{1}}只跟质量m{\displaystyle m}、力强度k{\displaystyle k}、总能量E{\displaystyle E}有关。不变量C1{\displaystyle C_{1}}分别与Di{\displaystyle D_{i}}，Li{\displaystyle L_{i}}的泊松括号等于零的导引并不明显。这不变量C1{\displaystyle C_{1}}使得只用到量子力学的正则对易关系，就可以推导出类氢原子的原子能级，而不必用到的薛定谔方程。

氢原子量子力学

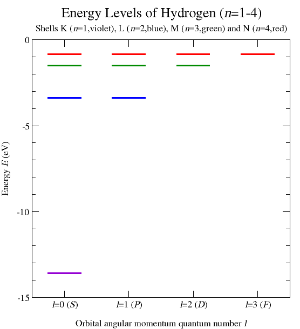
图6：从LRL矢量算符与角动量算符的对易关系，预测出来的氢原子的原子能级。各种实验都准确地证实这些能级正确无误。

泊松括号提供了一个简易的方法来正则量子化经典系统。两个量子算符的对易关系等于iℏ ℏ -->{\displaystyle i\hbar }乘以对应的经典变量。经过这量子化程序，计算开普勒问题的卡西米尔算符C1{\displaystyle C_{1}}的本征值，沃尔夫冈·包利成功地推导出类氢原子的原子能级（参阅图6），发射光谱射光谱。早在薛定谔方程成立之前，包利就研究出这重要的结果！

LRL矢量A{\displaystyle \mathbf {A} }的量子算符有一个奥妙之处，那就是动量算符与角动量算符并不对易。动量与角动量的叉积必须仔细地加以定义。LRL矢量的直角坐标分量典型地定义为

其中，me{\displaystyle m_{e}}是电子的质量，常数α α -->=e24π π -->ϵ ϵ -->0{\displaystyle \alpha ={\frac {e^{2}}{4\pi \epsilon _{0}}}}，e{\displaystyle e}是单位电荷量，ϵ ϵ -->0{\displaystyle \epsilon _{0}}是真空电容率。

这定义有一个特性：指标i, j{\displaystyle i,\ j}是对称的，指标i, j{\displaystyle i,\ j}的互换不会改变Ak{\displaystyle A_{k}}的数值。表示为矢量形式，

那么，其对应的哈密顿算符是

与A{\displaystyle \mathbf {A} }矢量成正比的D{\displaystyle \mathbf {D} }矢量则是

请注意，由于哈密顿算符的本征值是负值，所以公式内的平方根是个实数。

经过一番繁冗的运算，可以求得对易关系：

定义第一阶张量算符为

一个归一化的第一卡西米尔算符可以同样地定义为

注意到J+1{\displaystyle J_{+1}}和J− − -->1{\displaystyle J_{-1}}的对易关系是

应用维格纳-艾卡定理（Wigner-Eckart theorem），

其中，|l,m⟩ ⟩ -->{\displaystyle |l,\,m\rangle角量子数量子数为l{\displaystyle 磁量子数量子数为l{\displaystyle l}的本征态，Cl{\displaystyle {\mathfrak {C}}_{l}}是常数系数。

经过一番运算，J+1{\displaystyle J_{+1}}和J− − -->1{\displaystyle J_{-1}}的对易算符作用于|l,m⟩ ⟩ -->{\displaystyle |l,\,m\rangle }的结果是

所以，Cl{\displaystyle {\mathfrak {C}}_{l}}的递回关系是

假设Cl2{\displaystyle {\mathfrak {C}}_{l}^{2}}是非负值，则为了满足上述公式，l>0{\displaystyle l>0}。再假设l{\displaystyle l}的最大值是lmax{\displaystyle l_{max}}。由于态矢量|lmax+1, ⟩ ⟩ -->{\displaystyle |l_{max}+1,\,\ \rangle }不存在，Clmax+1=0{\displaystyle {\mathfrak {C}}_{l_{max}+1}=0}。因此，Clmax=ℏ ℏ -->22lmax− − -->1{\displaystyle {\mathfrak {C}}_{l_{max}}={\frac {\hbar ^{2}}{2l_{max}-1}}}。设定n=lmax− − -->1{\displaystyle n=l_{max}-1}，稍加计算，Cl{\displaystyle {\mathfrak {C}}_{l}}的一般方程为

这个n{\displaystyle n}就是跟能级有关的主量子数。先计算D2{\displaystyle D^{2}}：

所以，第一卡西米尔算符C1{\displaystyle C_{1}}作用于态矢量|n,l,m⟩ ⟩ -->{\displaystyle |n,\,l,\,m\rangle }可以得到

第一卡西米尔算符C1{\displaystyle C_{1}}的本征值是(n2− − -->1)ℏ ℏ -->2{\displaystyle (n^{2}-1)\hbar ^{2}}。重点是，这些本征值跟量子数l{\displaystyle l}、m{\displaystyle m}无关，这造成了原子能阶的简并：

这就是著名的氢原子玻尔公式。

保守性与对称性

在开普勒问题里，LRL矢量的保守性对应于系统的一种微妙的对称性。在经典力学里，对称性可以由连续运算显示出来；这连续运算可以将一个轨道映射至另外一个轨道，而同时保持系统的能量不变。在量子力学里，连续运算将同能级原子轨域混合在一起，也就是说，（简并原子能级）。

通常，对于每一个对称性都会存在有一个保守量。例如，有心力系统必对称于旋转群SO(3)；因而指引出角动量L{\displaystyle \mathbf {L} }的保守性。在经典力学里，整个系统的旋转不会影响轨道的能量。在量子力学里，假若旋转只混合角量子数相同的球谐函数，则系统的能量不会改变。

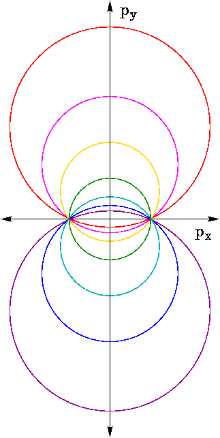
图7：同能量的动量的速端曲线家族。每一个圆圈都经过在px-轴上，同样的两点± ± -->p0=± ± -->2m|E|{\displaystyle \pm p_{0}=\pm {\sqrt {2m\left|E\right|}}}。这一家族的速端曲线对应于一个家族的阿波罗尼奥斯圆，和双极坐标的σ σ -->{\displaystyle \sigma }坐标曲面。

平方反比有心力系统的对称性是更高维与更微妙的。这奇特的对称性是由角动量L{\displaystyle \mathbf {L} }与LRL矢量A{\displaystyle \mathbf {A} }的双重保守性造成的；这保证了氢原子的能级跟角量子数l{\displaystyle l}、磁量子数m{\displaystyle m}无关。由于对称性运算必须发生于更高维空间，使得这对称性更加的微妙；这类的对称性常称为对称性。在经典力学里，开普勒问题的高维对称性容许连续的改变轨道．只要保持能量不变，而角动量可以改变；换句话说，同能量，不同角动量（离心率）的轨道可以互相的连续变换。在量子力学里，这对应着不同角量子数l{\displaystyle l}与磁量子数m{\displaystyle m}的轨域的混合，例如s(l=0){\displaystyle s(l=0)}与p(l=1){\displaystyle p(l=1)}原子轨域的混合。这种混合是不能用普通的三维平移运算或旋转运算达成的。可是，这种混合等价于高维度空间的旋转。

在一个束缚（bounded）系统里，能量是负值的，这高维对称群是SO(4)；特性是四维矢量的长度保持不变：

1935年，弗拉基米尔·佛克（Vladimir Fock）表明，在量子力学里，束缚的开普勒问题等价于一个粒子自由地移动于四维空间的三维单位球。更具体地，佛克表明，在开普勒问题的动量空间，薛定谔波函数是球谐函数的球极平面投影。圆球的旋转与重复射影造成了椭圆轨域的连续映射，同时维持能量不变；这对应于主量子数n{\displaystyle n}相同的轨域的混合。随后，华伦泰·巴格曼注意到，跟LRL矢量成比例的矢量D{\displaystyle \mathbf {D} }与角动量L{\displaystyle \mathbf {L} }的泊松括号形成SO(4)的李代数。简单地说，D{\displaystyle \mathbf {D} }与L{\displaystyle \mathbf {L} }的六个物理量对应于在四维空间里的六个保守的角动量分量，相伴于在四维空间里的六个合法的简单旋转（从四个轴中，选两个轴为旋转轴。一共有六种可能）。这结论并不意示宇宙是一个三维球面；而只是说，这个特别的物理问题（开普勒问题），在数学上，等价于移动于三维球面的一个自由粒子。

在一个非束缚（unbound），散射系统里，能量是正值的，对应的高维对称群是SO(3,1)；其特性是保持四维矢量的闵可夫斯基长度不变：

有心力系统（包括开普勒问题的那些系统）的轨道对于反射也具有对称性。所以，轨道的完全对称群并不是前面所提的SO(3)、SO(4)、SO(3,1)群；而分别是O(3)、O(4)、O(3,1)。然而，只需要连通子群SO(3)、SO(4)、SO(3,1)来展示出角动量与LRL矢量的保守性；反射对称性与保守性不相关。保守性可以由群的李代数推导出来。

旋转对称性在四维空间

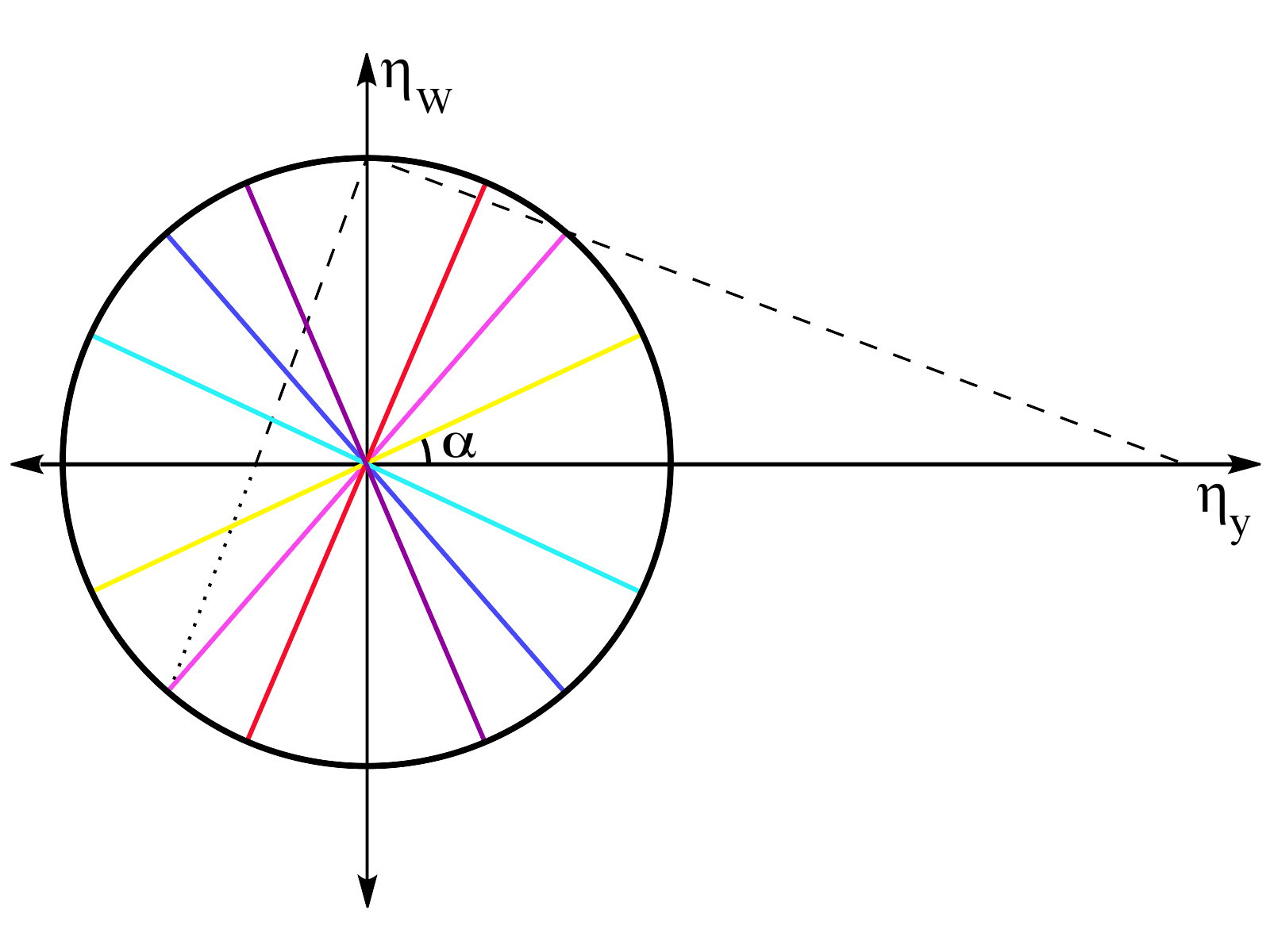
图8：图7的动量的速端曲线对应于η η -->{\displaystyle \eta }三维单位球的大圆线的球极平面投影。每一个大圆线都与η η -->x{\displaystyle \eta _{x}}-轴相交，后者垂直于页面。投影是从北极（w{\displaystyle w}单位矢量）到η η -->x{\displaystyle \eta _{x}}η η -->x{\displaystyle \eta _{x}}-平面，如同这里的虚黑线表示于品红色速端曲线。在纬度α α -->{\displaystyle \alpha }的大圆线对应于离心率e=sin α α -->{\displaystyle e=sin\ \alpha }。在这图里的大圆线的颜色对应于它们在图7的速端曲线。

开普勒问题与四维旋转对称性SO(4)的关联可以很容易地观察出来。标记四维直角坐标为(w, x, y, z){\displaystyle (w,\ x,\ y,\ z)}；其中，(x, y, z){\displaystyle (x,\ y,\ z)}代表三维位置矢量r{\displaystyle \mathbf {r} }的直角坐标。三维动量p{\displaystyle \mathbf {p} }与三维单位球的四维矢量η η -->{\displaystyle {\boldsymbol {\eta }}}的关系为

其中，w^ ^ -->{\displaystyle \mathbf {\hat {w}} }是新的w-轴的单位矢量。

很简单地，可以核对η η -->{\displaystyle {\boldsymbol {\eta }}}也是一个单位矢量：

从p{\displaystyle \mathbf {p} }至η η -->^ ^ -->{\displaystyle {\hat {\boldsymbol {\eta }}}}的映射有一个独特唯一的逆反；例如，动量p{\displaystyle \mathbf {p} }的x-轴分量是

py{\displaystyle p_{y}}与pz{\displaystyle p_{z}}也有类似的公式。换句话说，三维动量矢量p{\displaystyle \mathbf {p} }是四维单位矢量η η -->^ ^ -->{\displaystyle {\hat {\boldsymbol {\eta }}}}的球极平面投影，其比例因子为p0{\displaystyle p_{0}}。

选择一个合适的直角坐标，使z-轴与角动量L{\displaystyle \mathbf {L} }同直线，使动量的速端曲线的取向如同图7，圆心包含于y-轴。这样，不失广义性，就可以观察到这旋转对称性。由于粒子的运动包含于一个平面，p{\displaystyle \mathbf {p} }与L{\displaystyle \mathbf {L} }互相垂直，而且，pz=η η -->z=0{\displaystyle p_{z}=\eta _{z}=0}。因此，只需要专注于三维矢量η η -->^ ^ -->=(η η -->w, η η -->x, η η -->y){\displaystyle {\hat {\boldsymbol {\eta }}}=(\eta _{w},\ \eta _{x},\ \阿波罗尼奥斯y})}。图7速端曲线的阿波罗尼奥斯圆家族对应于在三维单位球η η -->{\displaystyle {\boldsymbol {\eta }}}的大圆线家族。每一个大圆线与η η -->x{\displaystyle \eta _{x}}相交于两个交点η η -->x=± ± -->1{\displaystyle \eta _{x}=\pm 1}。这两个交点相对于速端曲线图的两点px=± ± -->p0{\displaystyle p_{x}=\pm p_{0}}。这两个交点也是这些大圆线的共同交点。所以，这些大圆线的互相关系是一个环绕着η η -->x{\displaystyle \eta _{x}}-轴的简单旋转（参阅图8）。以η η -->x{\displaystyle \eta _{x}}-轴为转轴，每一个大圆线的位置是从η η -->xη η -->y{\displaystyle \eta _{x}\eta _{y}}-平面旋转α α -->{\displaystyle \alpha }角。

取任意一个大圆线η η -->y{\displaystyle \eta _{y}}最大值的一点，其坐标为(η η -->w, 0, η η -->y, 0){\displaystyle (\eta _{w},\ 0,\ \eta _{y},\ 0)}。那么，

经过一番运算，代入p0{\displaystyle p_{0}}的值，可以得到

给予一个束缚轨道，能量是负值的：

所以，离心率e=sin⁡ ⁡ -->(α α -->){\displaystyle e=\sin(\alpha )}是纬度α α -->{\displaystyle \alpha }的正弦函数。

由于图7的动量的速端曲线对应于η η -->{\displaystyle \eta }三维单位球的大圆线的球极平面投影，而这速端曲线家族的成员都拥有相同的能量。所以，这旋转的对称性使所有能量相同的轨道都能够互相变换。但是，这旋转正交于通常的三维旋转，因为它涉及了第四维η η -->w{\displaystyle \eta _{w}}。高维度的对称性是开普勒问题对应于LRL矢量的一个特征。

采用椭圆柱坐标χ χ -->, ψ ψ -->, ϕ ϕ -->{\displaystyle \chi ,\ \psi ,\ \phi }来代替四维坐标η η -->{\displaystyle {\boldsymbol {\eta }}}，开普勒问题有一个精致的作用量-角度坐标解答：

其中，sn,cn,dn{\displaystyle \mathrm {sn} ,\,\mathrm {cn} ,\,\mathrm {dn} }是亚可比椭圆函数。

开普勒问题LRL矢量恒定的证明

以下几种导引可以证明，在平方反比有心力下，LRL矢量守恒。

直接证明

假设，一个有心力f(r)r^ ^ -->{\displaystyle f(\mathbf {r} ){\hat {\mathbf {r} }}}作用于一个粒子。根据牛顿第二定律，运动方程为

其中，f(r){\displaystyle f(\mathbf {r} )}是函数，r{\displaystyle \mathbf {r} }为粒子的位置，p{\displaystyle \mathbf {p} }是动量，t{\displaystyle t}是时间。

由于在有心力下，角动量L=r× × -->p{\displaystyle \mathbf {L} =\mathbf {r} \times \mathbf {p} }是恒定的，

所以，

代入以下恒等式：

可以得到方程，

代入平方反比有心力的方程f(r)=− − -->kr2{\displaystyle f(\mathbf {r} )={\frac {-k}{r^{2}}}}，

所以，在平方反比有心力下，A{\displaystyle \mathbf {A} }是恒定的：

哈密顿-亚可比方程

哈密顿-亚可比方程的可分性也可以用推导出LRL矢量的恒定性。采用抛物线坐标(ξ ξ -->, η η -->){\displaystyle (\xi ,\ \eta )}，定义

其中，(x, y){\displaystyle (x,\ y)}是直角坐标，r{\displaystyle r}是轨道的径向距离：

逆反过来，

则开普勒问题的哈密顿量为

其中，pξ ξ -->, pη η -->{\displaystyle p_{\xi },\ p_{\eta }}分别是广义坐标ξ ξ -->, η η -->{\displaystyle \xi ,\ \eta }的共轭动量。

由于开普勒问题的势函数只跟广义坐标有关，哈密顿量是个能量运动常数，H=E{\displaystyle H=E}。稍加编排，可以得到

这公式的左手边与右手边分别跟不同的广义坐标有关，所以，两边都相等于一个运动常数，标记为Γ Γ -->{\displaystyle \Gamma }：

思考LRL矢量的x{\displaystyle x}分量，

代入能量方程E=12mv2− − -->kr{\displaystyle E={\frac {1}{2}}mv^{2}-{\frac {k}{r}}}，则

这公式右手边，前三个项目，经过一番计算，可以得到

所以，Ax{\displaystyle A_{x}}也是运动常数：

诺特定理

LRL矢量的保守性与前面所提的旋转对称性，两者之间的关系，可以用诺特定理来做连结分析。诺特定理也可以用来辨明LRL矢量是运动常数。诺特定理表明：在一个物理系统里，对于广义坐标qi{\displaystyle q_{i}}的微小变分δ δ -->qi=ϵ ϵ -->gi(q, q˙ ˙ -->, t){\displaystyle \delta q_{i}=\epsilon g_{i}(\mathbf {q} ,\ \mathbf {\dot {q}} ,\ t)}，假若，取至微小参数ϵ ϵ -->{\displaystyle \epsilon }的一阶，拉格朗日量L{\displaystyle {\mathcal {L}}}的变分δ δ -->L{\displaystyle \delta {\mathcal {L}}}是

则必存在保守量Γ Γ -->{\displaystyle \Gamma }满足方程

其中，gi(q, q˙ ˙ -->, t){\displaystyle g_{i}(\mathbf {q} ,\ \mathbf {\dot {q}} ,\ t)}、G(q, t){\displaystyle G(\mathbf {q} ,\ t)}都是函数。

更具体地，在一个开普勒问题里，试设定坐标xi{\displaystyle x_{i}}的微小变分为

其中，i=1, 2, 3{\displaystyle i=1,\ 2,\ 3}，xi{\displaystyle x_{i}}与pi{\displaystyle p_{i}}分别为位置r{\displaystyle \mathbf {r} }与动量p{\displaystyle \mathbf {p} }的i{\displaystyle i}-轴分量，δ δ -->is{\displaystyle \delta _{is}}是克罗内克尔δ，s{\displaystyle s}是固定的下标。

由于开普勒问题的拉格朗日量是

其运动方程为

对应于坐标xi{\displaystyle x_{i}}的变分，速度x˙ ˙ -->i{\displaystyle {\dot {x}}_{i}}的变分为

拉格朗日量取至一阶的变分是

代入δ δ -->xi{\displaystyle \delta x_{i}}和δ δ -->x˙ ˙ -->i{\displaystyle \delta {\dot {x}}_{i}}的公式，经过一番繁琐的运算，可以得到

再代入保守量Γ Γ -->{\displaystyle \Gamma }的公式，则会得到

而这正是LRL矢量的s{\displaystyle s}-轴分量As{\displaystyle A_{s}}。

李变换

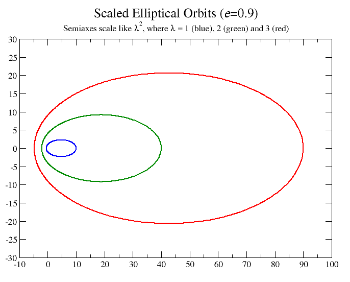
图9:推导出LRL矢量保守性的李变换。当这比例参数λ λ -->{\displaystyle \lambda }改变时，能量与角动量的大小也一起改变，可是离心率e{\displaystyle e}与LRL矢量A{\displaystyle \mathbf {A} }的大小与方向不变。

诺特定理精致地推导出LRL矢量的保守性。美中不足地，这导引有一个弱点：坐标变分δ δ -->xi{\displaystyle \delta x_{i}}不只涉及了位置r{\displaystyle \mathbf {r} }，而且还涉及了动量p{\displaystyle \mathbf {p} }。假若，使用索菲斯·李斯·李创建的方法来推导，可以除去这弱点。具体地，定义一个李变换，坐标r{\displaystyle \mathbf {r} }与时间t{\displaystyle t}都按照比例变换，比例是参数λ λ -->{\displaystyle \lambda }的不同羃数：

这变换改变了角动量L{\displaystyle L}的大小与能量E{\displaystyle E}：

可是，仍旧保持乘积EL2{\displaystyle EL^{2}}不变。所以，离心率e{\displaystyle e}与LRL矢量A{\displaystyle \mathbf {A} }的大小不变。这可以从A2{\displaystyle A^{2}}的公式观察出：

由于半短轴与半长轴的取向不因整体的比例变换而改变，LRL矢量A{\displaystyle \mathbf {A} }的方向也会保持不变。在李变换下，开普勒第三定律也仍旧成立：半长轴a{\displaystyle a}与周期T{\displaystyle T}形成常数T2/a3{\displaystyle {T^{2}}/{a^{3}}}。

推广至别种位势和相对论

LRL矢量可以推广至其他状况；可以用来辨认在其他状况下的保守值。

假设，一个物理系统里，存在着电场E{\displaystyle \mathbf {E} }，保守的广义LRL矢量A{\displaystyle {\mathcal {A}}}是

其中，q{\displaystyle q}是粒子的电荷量。

最广义的LRL矢量的形式可以表达为

其中，u=1r{\displaystyle u={\frac {1}{r}}}（参阅伯特兰定理），ξ ξ -->=cos⁡ ⁡ -->θ θ -->{\displaystyle \xi =\cos \theta }，角θ θ -->{\displaystyle \theta }定义为

其中，γ γ -->{\displaystyle \gamma洛伦兹因子兹因子。

如同前面所提，计算L{\displaystyle \mathbf {L} }与A{\displaystyle {\mathcal {A}}}的叉积，可以得到一个保守的副法线矢量B{\displaystyle {\mathcal {B}}}：

综和两个矢量成为一个保守的并矢张量W{\displaystyle {\mathcal {W}}}：

举例说明，计算一个非相对论性，均向性谐振子的LRL矢量。由于作用力是有心力，F(r)=− − -->kr{\displaystyle \mathbf {F} (r)=-k\mathbf {r} }，力子的角动量是保守的，粒子的运动包含于一个平面。请注意，P{\displaystyle \mathbf {P} }与L{\displaystyle \mathbf {L} }不是一定互相垂直的。保守的并矢张量可以表达为一个简单的形式：

其相应的LRL矢量必较复杂

其中，ω ω -->0=km{\displaystyle \omega _{0}={\sqrt {\frac {k}{m}}}}是自然振率。

别种比例与表述

不同于动量与角动量，并没有学术界一致认同的LRL矢量定义；在科学文献里，存在有几种不同的比例因子与符号。前面所述的定义是最普遍的定义。另外一种常见的定义，将A{\displaystyle \mathbf {A} }除以常数mk{\displaystyle mk}；这样，可以得到一个无量纲的离心率矢量e{\displaystyle \mathbf {e} }：

其中，v{\displaystyle \mathbf {v} }是速度。

离心率矢量e{\displaystyle \mathbf {e} }的方向与A{\displaystyle \mathbf {A} }相同，大小是轨道的离心率。

别种比例的版本也可能会用到。例如，将A{\displaystyle \mathbf {A} }除以m{\displaystyle m}：

或者，将A{\displaystyle \mathbf {A} }除以P0{\displaystyle P_{0}}：

D{\displaystyle \mathbf {D} }与角动量L{\displaystyle \mathbf {L} }的单位相同。在非常稀有的状况，LRL矢量的正负号会改变。这些，都不会影响它是运动常数的事实。

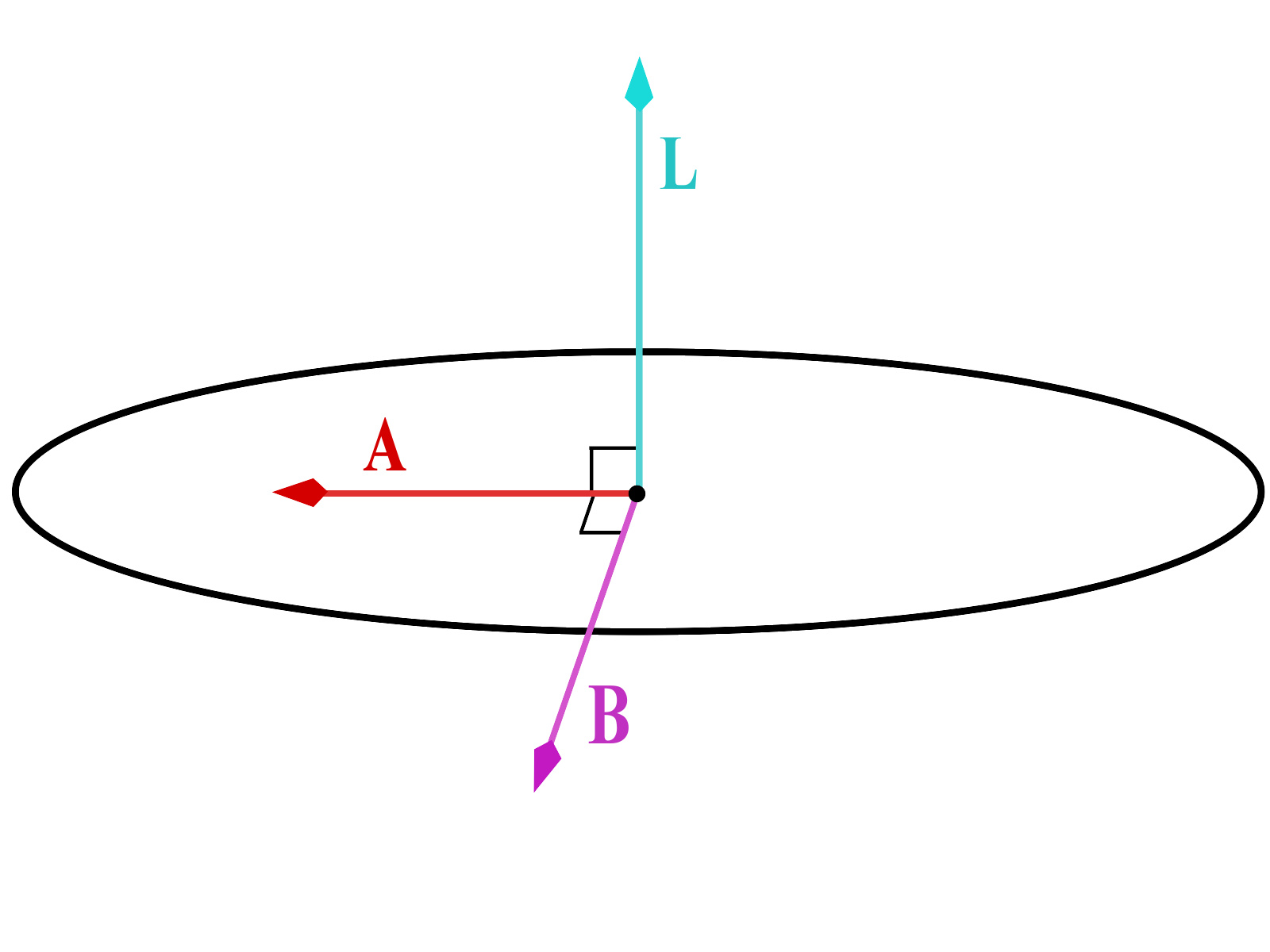
图4:角动量L{\displaystyle \mathbf {L} }，LRL矢量A{\displaystyle \mathbf {A} }，与副法线矢量B{\displaystyle \mathbf {B} }都互相垂直。A{\displaystyle \mathbf {A} }与B{\displaystyle \mathbf {B} }分别和椭圆的半长轴与半短轴的指向相同。

另外一个保守的矢量是副法线矢量B{\displaystyle \mathbf {B} }。威廉·哈密顿曾经研究过这矢量。

这保守的矢量与椭圆的半短轴同直线。A{\displaystyle \mathbf {A} }是B{\displaystyle \mathbf {B} }叉积L{\displaystyle \mathbf {L} }（参阅图4）。两个矢量A{\displaystyle \mathbf {A} }与B{\displaystyle \mathbf {B} }可以结合起来形成一个保守的并矢张量W{\displaystyle {\mathcal {W}}}：

其中，α α -->{\displaystyle \alpha }与β β -->{\displaystyle \beta }是任意比例常数，符号 ⊗ ⊗ -->{\displaystyle \otimes }表示张量积。展开这公式为

由于两个矢量互相垂直，A{\displaystyle \mathbf {A} }与B{\displaystyle \mathbf {B} }可以视为保守的张量W{\displaystyle {\mathcal {W}}}的主轴，也就是说，按比例的特征矢量。由于A{\displaystyle \mathbf {A} }与B{\displaystyle \mathbf {B} }都垂直于L{\displaystyle \mathbf {L} }，张量W{\displaystyle {\mathcal {W}}}垂直于角动量L{\displaystyle \mathbf {L} }：

参阅

二体问题

伯特兰定理

量子力学

航天动力学：轨道，离心率矢量，轨道根数

参考文献

Leach, P.G.L.; G.P. Flessas, Generalisations of the Laplace–Runge–Lenz vector, J. Nonlinear Math. Phys., 2003, 10: 340–423,arXiv:math-ph/0403028 

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。