文氏图

起源

剑桥大学冈维尔与凯斯学院餐厅的彩色玻璃窗

约翰·维恩是19世纪英国的哲学家和数学家，他在1881年发明了文氏图。

例子

在文氏图法中，如果有论域，则以一个矩形框（的内部区域）表示论域；各个集合（或类）就以圆／椭圆（的内部区域）来表示。两个圆／椭圆相交，其相交部分表示两个集合（或类）的公共元素，两个圆／椭圆不相交（相离或相切，而实际上在文氏图中相切是没有什么意义的，因为 文氏图是以图形的内部区域来表示的 ）则说明这两个集合（或类）没有公共元素。

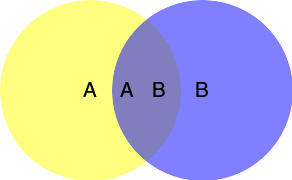
集合A和B

比如黄色的圆圈（集合 A ）可以表示两足的所有活物。蓝色的圆圈（集合 B ）可以表示会飞的所有活物。黄色和蓝色的圆圈交叠的区域（叫做交集）包含会飞 且 两足的所有活物──比如鹦鹉。（把每个单独的活物类型想像为在这个图中的某个点）。

人和企鹅会在橙色圆圈中不与蓝色圆圈交叠的部分中。蚊子有六足并且会飞，所以蚊子的点可以在蓝色圆圈中不与橙色圆圈交叠的部分中。不是两足并且不会飞的东西（比如鲸和响尾蛇）可以表示为在这两个圆圈之外的点。在技术上，上面的文氏图可以解释为"集合 A 和集合 B 之间的联系，它们可以有一些（但不是全部）的元素是公共的"。

集合 A 和 B 的组合区域叫做集合 A 和 B 的并集。在这个个例中并集包含要么两足、要么会飞、要么两足并且会飞的所有东西。圆圈交叠暗示着两个集合的交集非空──就是说在事实上 有 活物 同时 在黄色和蓝色圆圈中。

文氏图与其它的图示法一样，它不能准确表示一个集合（或类）中到底有哪些元素。

类似的图

欧拉图可能在外观上同文氏图是一致的。它们之间的区别只在于它们的应用领域中，就是说在被分割的全集的类型中。欧拉图展示 对象 的特定集合，文氏图的概念更一般的适用于可能的联系。文氏图和欧拉图没有合并的原因可能是，欧拉的版本是早在100多年前就出现了的，欧拉已经有了足够多的成就了，而Venn只留下了这么一个图。

在欧拉图和文氏图之间的区别只是在想法上，欧拉图要展示特定集合之间的联系，而文氏图要包含所有可能的组合。下面是欧拉图的一个例子：

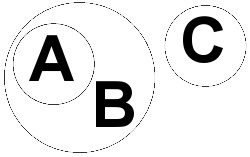
集合A, B和C

在这个例子中，一个集合完全在另一个集合内部。我们说集合 A 是在世界中能找到的所有的不同类型的奶酪，集合 B 是在世界中能找到的所有食物。从这个图中，你可以看出所有奶酪都是食物，但是不是所有食物都是奶酪。进一步的说，集合 C （比如说金属造物）与集合 B 没有公共元素（集合的成员），从此我们可以在逻辑上断言没有奶酪是金属造物（或者反过来说）。在形式上，上述的图可以在数学上解释为"集合 A 是集合 B 的真子集，而集合 C 和集合 B 没有公共元素"。

或解释为一个三段论

所有 A s是 B s

没有 C s是 B s

所以，没有 C s是 A s

所以，没有 A s是 C s。

扩展到更多个集合

历来有许多把文氏图推广到多个集合的尝试。Venn使用椭圆达到了四个集合但从未满意他的五集合解法。在一个世纪之后，才找到了一种能满足Venn关于对称性的非正式要求。这是A. W. F. Edwards在设计彩色玻璃窗以缅怀Venn的时候，所得出的‘齿轮’方法：

在大众文化中

在美国电视剧生活大爆炸（The Big Bang Theory）S1E14中，Leonard不小心买下了巨型时光机，他纳闷道：谁会用800元就卖出一台全尺寸的时间机器？ Sheldon回答：在文氏图中，那是位于“不再想要时间机器”和“需要800元”两个集合的交接区域。

参见

图

布林代数

卡诺图

图形组织器

米尼佛夫人问题

与文氏图类似的欧拉图

外部链接

What is a Venn diagram?

LogicTutorial.com- interactive Johnston diagram

Lewis Carroll"s Logic Game- Venn vs. Euler

A Survey of Venn Diagrams

Venn Diagrams

Region Identification in Venn Diagrams

英文版维基百科介绍

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。