同调论

简单解释

直觉上，同调是取一个等价关系，如果链 C - D 是一个高一维链的边界，则链 C 与 D 是同调的。最简单的例子是在图论中，有 C 和 D 两组顶点集，考虑到从 P到 Q 的有向边 E 的边缘是 Q-P。从 D 到 C 的一些边的集合，每一个与前一个相连，是一个同调。

一般的，一个 k-链视为形式组合

其中 ai{\displaystyle a_{i}} 是整数而 di{\displaystyle d_{i}} 是 X 上的 k-维单形。这里的边缘取一个单形的边界；它导致一个高维概念，k=1 即类似于图论情形中的裂项和。这个解释是1900年的风格，从技术上讲有些原始。

以环面为例

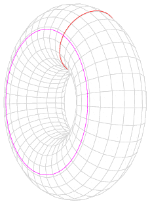
例如，若 X 是一个二维环面T，T 上一个一维圈从直觉来说是 T 中曲线之线性组合，且这些曲线是闭合的（圈条件，等价于没有边界）。如果 C 与 D 是以同样方式绕 T 一周的圈，则我们可清晰地找出 T 上一个定向区域其边界是 C − D。可以证明整系数 1-圈的同调类构成一个有两个生成元的自由阿贝尔群，他们是绕此环面的两种不同方式。

十九世纪

这种层次的理解是十九世纪数学界中的共有性质，源于黎曼曲面的想法。十九世纪末，庞加莱给出了一个更一般但仍基于直觉的背景。

例如，考虑最先由庞加莱于1899年表述的一般斯托克斯定理：它必须涉及一个积分项（现在我们称为微分形式）和一个积分区域（一个 p-链），以及两类边缘算子，一个用现代术语是外微分，另一个是链上包含了定向的几何边缘算子，它可用于同调论。这两个算子是关于积分是伴随算子。

二十世纪

粗糙地讲，对同调的几何论证直到二十世纪初才被严格的技术取代。起先时代的特色是使用组合拓扑（今日代数拓扑的先驱）。这假设了所处理的空间是单纯复形，但最感兴趣的空间通常是流形，故人为的三角化被引入了这个工具。始创者们比如所罗门·莱夫谢茨以及马斯顿·莫尔斯仍更偏好几何方法。组合观点使布劳威尔能证明比如单纯逼近定理之类的基本结论，基于同调是一个函子的想法。布劳威尔使用这个新工具能证明复分析基础的若尔当曲线定理，以及区域不变性；并消除了对拓扑论证的怀疑。

代数拓扑学

通常将到“代数”拓扑的转变归功于埃米·诺特的影响，她坚持同调类属于商群——这种观点是基本的，现在已经作为定义。事实上从1920年以来诺特与她的学生建立了任何环的模理论，这两种想法融合形成了系数取值于一个环的同调的概念。在此之前，系数（即链是空间上的基本几何链的线性组合的系数）通常是整数、实数或复数，或者有时为模2同余类。在新的情形下，没有理由不取模3同余类，例如：成为一个圈需满足更复杂的几何条件，例如图论中在每个顶点的边数都是3的倍数。但在代数几何中，定义没有任何新问题。万有系数定理指出整系数同调决定了所以其它同调理论，但利用了张量积；这不是止痛剂，在张量积有导出函子，导致一个一般的表述。

上同调与奇异同调

1930年代是上同调论发展的十年，多个研究方向一起成长，而上面讲过在庞加莱工作中不明确的德拉姆上同调成为一个清楚的定理。上同调与同调是对偶理论；同时得知同调论，单纯同调，远非它故事的结束。奇异同调的定义避开了明显的三角化，其代价是引入无限生成模。

公理化与异常理论

从1940年到1960年，代数拓扑迅速地发展，同调论的角色通常作为基本理论，容易计算，拓扑学家用它去计算其它函子。艾伦伯格与斯廷罗德的同调论公理化（艾伦伯格-斯廷罗德公理）揭示了同调理论的不同候选通常是，粗糙地讲，某些正合序列特别是迈耶-菲托里斯序列，以及算出了一个点的同调的维数公理。在拓扑K-理论与配边理论中导出的（上）同调，在同伦论中成为标准的推广到异常（上）同调论，中维数公里减弱了。他们对CW复形范畴容易刻画。

上同调论列表（List of cohomology theories）

同调论现状

对更一般（即不那么良态）的空间，借助于从层论中的想法得到同调论的许多推广，特别是局部紧空间的博雷尔-穆尔同调。

同调论的基本链复形转置很久以前就成为了同调代数中独立的一种技巧，并独立地应用于例如群上同调。从而在数学中不再只有一个同调论，而是有许多同调和上同调论。

参考文献

Hilton, Peter,A Brief, Subjective History of Homology and Homotopy Theory in This Century, Mathematics Magazine, 1988, 60 (5): 282–291 

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。